Position

Location - where am I ?

Map of Europe with a 30° graticule in dark gray

A graticule (from Latin crāticula 'grill/grating'), on a map, is a graphical depiction of a coordinate system as a grid of lines, each line representing a constant coordinate value. It is thus a form of isoline, and is commonly found on maps of many kinds, at scales from local to global.

The term is almost always used to specifically refer to the parallels and meridians of latitude and longitude respectively in the geographic coordinate system. In modern usage, graticules are contrasted with grids, which display the eastings and northings of another coordinate reference system, such as Universal Transverse Mercator – usually the coordinate system in which the map is drawn.

Some cartographers have used the term "graticule" to refer not only to the visual lines, but to the system of latitude and longitude reference itself; however, in the era of geographic information systems, it is more accurate to call this the geographic coordinate system.

Uses and design

The graticule may serve several purposes on a map:

• Aid map users in estimating the coordinates of locations
• Aid map users in identifying locations with known coordinates
• Indicate the cardinal directions, especially on map projections in which these directions vary across the map (e.g. conic, pseudocylindrical, azimuthal) where a north arrow or compass rose would not be appropriate

These are usually secondary to the main purpose of the map, so graticules are often drawn to be relatively low in the visual hierarchy.

History

1482 reproduction of the world map in the Geography of Claudius Ptolemy

The graticule is of ancient origin, being almost as old as the concept of the spherical Earth, coordinate system for measuring geographic locations, and the map projection. Strabo, in his Geography (ca 20 AD), states that the maps in Eratosthenes's Geography Book 3 (3rd century BC, now lost) contained lines "drawn from west to east, parallel to the equatorial line" (thus the term parallel) Ptolemy's Geography (ca 150 AD) gives detailed instructions for drawing the parallels and meridians for his two projections.

The works of Ptolemy and other classical geographers were available to the scientists of medieval Islam. Some, such as al-Khwarizmi, further developed these works, including creating maps on a graticule of latitude and longitude.

During the European Middle Ages, graticules disappeared from the few maps that were produced; T and O maps in particular were more concerned with religious cosmology than accurate representation of location. The portolan charts of the 13th to 15th centuries were much more accurate, but used rhumb lines that were much more useful for sea navigation than latitude and longitude. At the same time, however, the rediscovery of Ptolemy and other classical knowledge of the shape and size of the Earth led to the recreation of some of the ancient maps with their graticules; the earliest extant copies of Ptolemy's Geography with his maps date to the 14th and 15th centuries. Starting in the 16th century, the graticule has been ubiquitous on global and continental scale maps.

The Song-dynasty (12th-century) Yu Ji Tu map, based on a grid with a 100 li (about 30 mile) spacing.

There is some debate over whether the Chinese and other Asians knew the world to be spherical prior to Western contact, but most maps appear to assume regions as flat. Although Chinese maps do not portray any concept of latitude and longitude, cartesian grids appear on some maps dating back to the 11th century.

See also

• Projected coordinate system

This article is about the geographical reference system. For other uses, see Latitude (disambiguation).

Earth's graticule. The vertical lines from pole to pole are lines of constant longitude, or meridians. The circles parallel to the equator are lines of constant latitude, or parallels. The graticule shows the latitude and longitude of points on the surface. In this example meridians are spaced at 6° intervals and parallels at 4° intervals.

In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.

On its own, the term "latitude" normally refers to the geodetic latitude as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or normal) to the ellipsoidal surface from the point, and the plane of the equator.

Background

Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the oceans and its continuation under the land masses. The second step is to approximate the geoid by a mathematically simpler reference surface. The simplest choice for the reference surface is a sphere, but the geoid is more accurately modeled by an ellipsoid of revolution. The definitions of latitude and longitude on such reference surfaces are detailed in the following sections. Lines of constant latitude and longitude together constitute a graticule on the reference surface. The latitude of a point on the actual surface is that of the corresponding point on the reference surface, the correspondence being along the normal to the reference surface, which passes through the point on the physical surface. Latitude and longitude together with some specification of height constitute a geographic coordinate system as defined in the specification of the ISO 19111 standard.

Since there are many different reference ellipsoids, the precise latitude of a feature on the surface is not unique: this is stressed in the ISO standard which states that "without the full specification of the coordinate reference system, coordinates (that is latitude and longitude) are ambiguous at best and meaningless at worst". This is of great importance in accurate applications, such as a Global Positioning System (GPS), but in common usage, where high accuracy is not required, the reference ellipsoid is not usually stated.

In English texts, the latitude angle, defined below, is usually denoted by the Greek lower-case letter phi (ϕ or φ). It is measured in degrees, minutes and seconds or decimal degrees, north or south of the equator. For navigational purposes positions are given in degrees and decimal minutes. For instance, The Needles lighthouse is at 50°39.734′ N 001°35.500′ W.

This article relates to coordinate systems for the Earth: it may be adapted to cover the Moon, planets and other celestial objects (planetographic latitude).

For a brief history, see History of latitude.

Determination

See also: Longitude determination

Further information: Celestial navigation § Latitude

In celestial navigation, latitude is determined with the meridian altitude method. More precise measurement of latitude requires an understanding of the gravitational field of the Earth, either to set up theodolites or to determine GPS satellite orbits. The study of the figure of the Earth together with its gravitational field is the science of geodesy.

Latitude on the sphere

A perspective view of the Earth showing how latitude ($$

 
   
     
       ϕ
     
   
   {\displaystyle \phi }
 

) and longitude ($$

 
   
     
       λ
     
   
   {\displaystyle \lambda }
 

) are defined on a spherical model. The graticule spacing is 10 degrees.

The graticule on the sphere

The graticule is formed by the lines of constant latitude and constant longitude, which are constructed with reference to the rotation axis of the Earth. The primary reference points are the poles where the axis of rotation of the Earth intersects the reference surface. Planes which contain the rotation axis intersect the surface at the meridians; and the angle between any one meridian plane and that through Greenwich (the Prime Meridian) defines the longitude: meridians are lines of constant longitude. The plane through the centre of the Earth and perpendicular to the rotation axis intersects the surface at a great circle called the Equator. Planes parallel to the equatorial plane intersect the surface in circles of constant latitude; these are the parallels. The Equator has a latitude of 0°, the North Pole has a latitude of 90° North (written 90° N or +90°), and the South Pole has a latitude of 90° South (written 90° S or −90°). The latitude of an arbitrary point is the angle between the equatorial plane and the normal to the surface at that point: the normal to the surface of the sphere is along the radial vector.

The latitude, as defined in this way for the sphere, is often termed the spherical latitude, to avoid ambiguity with the geodetic latitude and the auxiliary latitudes defined in subsequent sections of this article.

Named latitudes on the Earth

The orientation of the Earth at the December solstice

Besides the equator, four other parallels are of significance:

Arctic Circle	66° 34′ (66.57°) N
Tropic of Cancer	23° 26′ (23.43°) N
Tropic of Capricorn	23° 26′ (23.43°) S
Antarctic Circle	66° 34′ (66.57°) S

The plane of the Earth's orbit about the Sun is called the ecliptic, and the plane perpendicular to the rotation axis of the Earth is the equatorial plane. The angle between the ecliptic and the equatorial plane is called variously the axial tilt, the obliquity, or the inclination of the ecliptic, and it is conventionally denoted by i. The latitude of the tropical circles is equal to i and the latitude of the polar circles is its complement (90° - i). The axis of rotation varies slowly over time and the values given here are those for the current epoch. The time variation is discussed more fully in the article on axial tilt.

The figure shows the geometry of a cross-section of the plane perpendicular to the ecliptic and through the centres of the Earth and the Sun at the December solstice when the Sun is overhead at some point of the Tropic of Capricorn. The south polar latitudes below the Antarctic Circle are in daylight, whilst the north polar latitudes above the Arctic Circle are in night. The situation is reversed at the June solstice, when the Sun is overhead at the Tropic of Cancer. Only at latitudes in between the two tropics is it possible for the Sun to be directly overhead (at the zenith).

On map projections there is no universal rule as to how meridians and parallels should appear. The examples below show the named parallels (as red lines) on the commonly used Mercator projection and the Transverse Mercator projection. On the former the parallels are horizontal and the meridians are vertical, whereas on the latter there is no exact relationship of parallels and meridians with horizontal and vertical: both are complicated curves.

	Normal Mercator		Transverse Mercator
		\

Latitude on the ellipsoid

Ellipsoids

Main article: Ellipsoid of revolution

In 1687 Isaac Newton published the Philosophiæ Naturalis Principia Mathematica, in which he proved that a rotating self-gravitating fluid body in equilibrium takes the form of an oblate ellipsoid. (This article uses the term ellipsoid in preference to the older term spheroid.) Newton's result was confirmed by geodetic measurements in the 18th century. (See Meridian arc.) An oblate ellipsoid is the three-dimensional surface generated by the rotation of an ellipse about its shorter axis (minor axis). "Oblate ellipsoid of revolution" is abbreviated to 'ellipsoid' in the remainder of this article. (Ellipsoids which do not have an axis of symmetry are termed triaxial.)

Many different reference ellipsoids have been used in the history of geodesy. In pre-satellite days they were devised to give a good fit to the geoid over the limited area of a survey but, with the advent of GPS, it has become natural to use reference ellipsoids (such as WGS84) with centre at the centre of mass of the Earth and minor axis aligned to the rotation axis of the Earth. These geocentric ellipsoids are usually within 100 m (330 ft) of the geoid. Since latitude is defined with respect to an ellipsoid, the position of a given point is different on each ellipsoid: one cannot exactly specify the latitude and longitude of a geographical feature without specifying the ellipsoid used. Many maps maintained by national agencies are based on older ellipsoids, so one must know how the latitude and longitude values are transformed from one ellipsoid to another. GPS handsets include software to carry out datum transformations which link WGS84 to the local reference ellipsoid with its associated grid.

The geometry of the ellipsoid

A sphere of radius a compressed along the z axis to form an oblate ellipsoid of revolution.

The shape of an ellipsoid of revolution is determined by the shape of the ellipse which is rotated about its minor (shorter) axis. Two parameters are required. One is invariably the equatorial radius, which is the semi-major axis, a. The other parameter is usually (1) the polar radius or semi-minor axis, b; or (2) the (first) flattening, f; or (3) the eccentricity, e. These parameters are not independent: they are related by

$f={\frac {a-b}{a}},\qquad e^{2}=2f-f^{2},\qquad b=a(1-f)=a{\sqrt {1-e^{2}}}\,.$

Many other parameters (see ellipse, ellipsoid) appear in the study of geodesy, geophysics and map projections but they can all be expressed in terms of one or two members of the set a, b, f and e. Both f and e are small and often appear in series expansions in calculations; they are of the order ⁠1/298⁠ and 0.0818 respectively. Values for a number of ellipsoids are given in Figure of the Earth. Reference ellipsoids are usually defined by the semi-major axis and the inverse flattening, ⁠1/f⁠. For example, the defining values for the WGS84 ellipsoid, used by all GPS devices, are

• a (equatorial radius): 6378137.0 m exactly
• ⁠1/f⁠ (inverse flattening): 298.257223563 exactly

from which are derived

• b (polar radius): 6356752.31425 m
• e² (eccentricity squared): 0.00669437999014

The difference between the semi-major and semi-minor axes is about 21 km (13 miles) and as fraction of the semi-major axis it equals the flattening; on a computer monitor the ellipsoid could be sized as 300 by 299 pixels. This would barely be distinguishable from a 300-by-300-pixel sphere, so illustrations usually exaggerate the flattening.

Geodetic and geocentric latitudes

See also: Geodetic coordinates § Geodetic vs. geocentric coordinates

The definition of geodetic latitude ($$

 
   
     
       ϕ
     
   
   {\displaystyle \phi }
 

) and longitude ($$

 
   
     
       λ
     
   
   {\displaystyle \lambda }
 

) on an ellipsoid. The normal to the surface does not pass through the centre, except at the equator and at the poles.

The graticule on the ellipsoid is constructed in exactly the same way as on the sphere. The normal at a point on the surface of an ellipsoid does not pass through the centre, except for points on the equator or at the poles, but the definition of latitude remains unchanged as the angle between the normal and the equatorial plane. The terminology for latitude must be made more precise by distinguishing:

• Geodetic latitude: the angle between the normal and the equatorial plane. The standard notation in English publications is ϕ. This is the definition assumed when the word latitude is used without qualification. The definition must be accompanied with a specification of the ellipsoid.
• Geocentric latitude (also known as spherical latitude, after the 3D polar angle): the angle between the radius (from centre to the point on the surface) and the equatorial plane. (Figure below). There is no standard notation: examples from various texts include θ, ψ, q, ϕ′, ϕ_c, ϕ_g. This article uses θ.

Geographic latitude must be used with care, as some authors use it as a synonym for geodetic latitude whilst others use it as an alternative to the astronomical latitude. "Latitude" (unqualified) should normally refer to the geodetic latitude.

The importance of specifying the reference datum may be illustrated by a simple example. On the reference ellipsoid for WGS84, the centre of the Eiffel Tower has a geodetic latitude of 48° 51′ 29″ N, or 48.8583° N and longitude of 2° 17′ 40″ E or 2.2944°E. The same coordinates on the datum ED50 define a point on the ground which is 140 metres (460 feet) distant from the tower. A web search may produce several different values for the latitude of the tower; the reference ellipsoid is rarely specified.

Meridian distance

Main article: Meridian arc

See also: Length of a degree of longitude

The length of a degree of latitude depends on the figure of the Earth assumed.

Meridian distance on the sphere

On the sphere the normal passes through the centre and the latitude (ϕ) is therefore equal to the angle subtended at the centre by the meridian arc from the equator to the point concerned. If the meridian distance is denoted by m(ϕ) then

$m(\phi )={\frac {\pi }{180^{\circ }}}R\phi _{\mathrm {degrees} }=R\phi _{\mathrm {radians} }$

where R denotes the mean radius of the Earth. R is equal to 6,371 km or 3,959 miles. No higher accuracy is appropriate for R since higher-precision results necessitate an ellipsoid model. With this value for R the meridian length of 1 degree of latitude on the sphere is 111.2 km (69.1 statute miles) (60.0 nautical miles). The length of one minute of latitude is 1.853 km (1.151 statute miles) (1.00 nautical miles), while the length of 1 second of latitude is 30.8 m or 101 feet (see nautical mile).

Meridian distance on the ellipsoid

In Meridian arc and standard texts it is shown that the distance along a meridian from latitude ϕ to the equator is given by (ϕ in radians)

$m(\phi )=\int _{0}^{\phi }M(\phi ')\,d\phi '=a\left(1-e^{2}\right)\int _{0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '$

where M(ϕ) is the meridional radius of curvature.

The quarter meridian distance from the equator to the pole is

$m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,$

For WGS84 this distance is 10001.965729 km.

The evaluation of the meridian distance integral is central to many studies in geodesy and map projection. It can be evaluated by expanding the integral by the binomial series and integrating term by term: see Meridian arc for details. The length of the meridian arc between two given latitudes is given by replacing the limits of the integral by the latitudes concerned. The length of a small meridian arc is given by

$\delta m(\phi )=M(\phi )\,\delta \phi =a\left(1-e^{2}\right)\left(1-e^{2}\sin ^{2}\phi \right)^{-{\frac {3}{2}}}\,\delta \phi$

$$ ϕ {\displaystyle \phi }	Δ1 lat	Δ1 long
0°	110.574 km	111.320 km
15°	110.649 km	107.550 km
30°	110.852 km	96.486 km
45°	111.132 km	78.847 km
60°	111.412 km	55.800 km
75°	111.618 km	28.902 km
90°	111.694 km	0.000 km

When the latitude difference is 1 degree, corresponding to ⁠π/180⁠ radians, the arc distance is about

$\Delta _{\text{lat}}^{1}={\frac {\pi a\left(1-e^{2}\right)}{180^{\circ }\left(1-e^{2}\sin ^{2}\phi \right)^{\frac {3}{2}}}}$

The distance in metres (correct to 0.01 metre) between latitudes $\phi$ − 0.5 degrees and $\phi$ + 0.5 degrees on the WGS84 spheroid is

$\Delta _{\text{lat}}^{1}=111\,132.954-559.822\cos 2\phi +1.175\cos 4\phi$

The variation of this distance with latitude (on WGS84) is shown in the table along with the length of a degree of longitude (east–west distance):

$\Delta _{\text{long}}^{1}={\frac {\pi a\cos \phi }{180^{\circ }{\sqrt {1-e^{2}\sin ^{2}\phi }}}}\,$

A calculator for any latitude is provided by the U.S. Government's National Geospatial-Intelligence Agency (NGA).

The following graph illustrates the variation of both a degree of latitude and a degree of longitude with latitude.

The definition of geodetic latitude (ϕ) and geocentric latitude (θ).

Auxiliary latitudes

There are six auxiliary latitudes that have applications to special problems in geodesy, geophysics and the theory of map projections:

• Geocentric latitude
• Parametric (or reduced) latitude
• Rectifying latitude
• Authalic latitude
• Conformal latitude
• Isometric latitude

The definitions given in this section all relate to locations on the reference ellipsoid but the first two auxiliary latitudes, like the geodetic latitude, can be extended to define a three-dimensional geographic coordinate system as discussed below. The remaining latitudes are not used in this way; they are used only as intermediate constructs in map projections of the reference ellipsoid to the plane or in calculations of geodesics on the ellipsoid. Their numerical values are not of interest. For example, no one would need to calculate the authalic latitude of the Eiffel Tower.

The expressions below give the auxiliary latitudes in terms of the geodetic latitude, the semi-major axis, a, and the eccentricity, e. (For inverses see below.) The forms given are, apart from notational variants, those in the standard reference for map projections, namely "Map projections: a working manual" by J. P. Snyder. Derivations of these expressions may be found in Adams and online publications by Osborne and Rapp.

Geocentric latitude

See also: § Geodetic and geocentric latitudes

The definition of geodetic latitude (ϕ) and geocentric latitude (θ)

The geocentric latitude is the angle between the equatorial plane and the radius from the centre to a point of interest.

When the point is on the surface of the ellipsoid, the relation between the geocentric latitude (θ) and the geodetic latitude (ϕ) is:

$\theta (\phi )=\tan ^{-1}\left(\left(1-e^{2}\right)\tan \phi \right)=\tan ^{-1}\left((1-f)^{2}\tan \phi \right)\,.$

For points not on the surface of the ellipsoid, the relationship involves additionally the ellipsoidal height h:

$\theta (\phi ,h)=\tan ^{-1}\left({\frac {N(1-f)^{2}+h}{N+h}}\tan \phi \right)$

where N is the prime vertical radius of curvature. The geodetic and geocentric latitudes are equal at the equator and at the poles but at other latitudes they differ by a few minutes of arc. Taking the value of the squared eccentricity as 0.0067 (it depends on the choice of ellipsoid) the maximum difference of $\phi {-}\theta$ may be shown to be about 11.5 minutes of arc at a geodetic latitude of approximately 45° 6′.

Parametric latitude (or reduced latitude)

Definition of the parametric latitude (β) on the ellipsoid

The parametric latitude or reduced latitude, β, is defined by the radius drawn from the centre of the ellipsoid to that point Q on the surrounding sphere (of radius a) which is the projection parallel to the Earth's axis of a point P on the ellipsoid at latitude ϕ. It was introduced by Legendre and Bessel who solved problems for geodesics on the ellipsoid by transforming them to an equivalent problem for spherical geodesics by using this smaller latitude. Bessel's notation, u(ϕ), is also used in the current literature. The parametric latitude is related to the geodetic latitude by:

$\beta (\phi )=\tan ^{-1}\left({\sqrt {1-e^{2}}}\tan \phi \right)=\tan ^{-1}\left((1-f)\tan \phi \right)$

The alternative name arises from the parameterization of the equation of the ellipse describing a meridian section. In terms of Cartesian coordinates p, the distance from the minor axis, and z, the distance above the equatorial plane, the equation of the ellipse is:

${\frac {p^{2}}{a^{2}}}+{\frac {z^{2}}{b^{2}}}=1\,.$

The Cartesian coordinates of the point are parameterized by

$p=a\cos \beta \,,\qquad z=b\sin \beta \,;$

Cayley suggested the term parametric latitude because of the form of these equations.

The parametric latitude is not used in the theory of map projections. Its most important application is in the theory of ellipsoid geodesics, (Vincenty, Karney).

Rectifying latitude

See also: Rectifying radius

The rectifying latitude, μ, is the meridian distance scaled so that its value at the poles is equal to 90 degrees or ⁠π/2⁠ radians:

$\mu (\phi )={\frac {\pi }{2}}{\frac {m(\phi )}{m_{\mathrm {p} }}}$

where the meridian distance from the equator to a latitude ϕ is (see Meridian arc)

$m(\phi )=a\left(1-e^{2}\right)\int _{0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '\,,$

and the length of the meridian quadrant from the equator to the pole (the polar distance) is

$m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,.$

Using the rectifying latitude to define a latitude on a sphere of radius

$R={\frac {2m_{\mathrm {p} }}{\pi }}$

defines a projection from the ellipsoid to the sphere such that all meridians have true length and uniform scale. The sphere may then be projected to the plane with an equirectangular projection to give a double projection from the ellipsoid to the plane such that all meridians have true length and uniform meridian scale. An example of the use of the rectifying latitude is the equidistant conic projection. (Snyder, Section 16). The rectifying latitude is also of great importance in the construction of the Transverse Mercator projection.

Authalic latitude

See also: Authalic radius

The authalic latitude (after the Greek for "same area"), ξ, gives an equal-area projection to a sphere.

$\xi (\phi )=\sin ^{-1}\left({\frac {q(\phi )}{q_{\mathrm {p} }}}\right)$

where

${\begin{aligned}q(\phi )&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)\\[2pt]&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}+{\frac {1-e^{2}}{e}}\tanh ^{-1}(e\sin \phi )\end{aligned}}$

and

${\begin{aligned}q_{\mathrm {p} }=q\left({\frac {\pi }{2}}\right)&=1-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e}{1+e}}\right)\\&=1+{\frac {1-e^{2}}{e}}\tanh ^{-1}e\end{aligned}}$

and the radius of the sphere is taken as

$R_{q}=a{\sqrt {\frac {q_{\mathrm {p} }}{2}}}\,.$

An example of the use of the authalic latitude is the Albers equal-area conic projection.

Conformal latitude

The conformal latitude, χ, gives an angle-preserving (conformal) transformation to the sphere.

${\begin{aligned}\chi (\phi )&=2\tan ^{-1}\left[\left({\frac {1+\sin \phi }{1-\sin \phi }}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{e}\right]^{\frac {1}{2}}-{\frac {\pi }{2}}\\[2pt]&=2\tan ^{-1}\left[\tan \left({\frac {\phi }{2}}+{\frac {\pi }{4}}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{\frac {e}{2}}\right]-{\frac {\pi }{2}}\\[2pt]&=\tan ^{-1}\left[\sinh \left(\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\right)\right]\\&=\operatorname {gd} \left[\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi )\right]\end{aligned}}$

where gd(x) is the Gudermannian function. (See also Mercator projection.)

The conformal latitude defines a transformation from the ellipsoid to a sphere of arbitrary radius such that the angle of intersection between any two lines on the ellipsoid is the same as the corresponding angle on the sphere (so that the shape of small elements is well preserved). A further conformal transformation from the sphere to the plane gives a conformal double projection from the ellipsoid to the plane. This is not the only way of generating such a conformal projection. For example, the 'exact' version of the Transverse Mercator projection on the ellipsoid is not a double projection. (It does, however, involve a generalisation of the conformal latitude to the complex plane).

Isometric latitude

The isometric latitude, ψ, is used in the development of the ellipsoidal versions of the normal Mercator projection and the Transverse Mercator projection. The name "isometric" arises from the fact that at any point on the ellipsoid equal increments of ψ and longitude λ give rise to equal distance displacements along the meridians and parallels respectively. The graticule defined by the lines of constant ψ and constant λ, divides the surface of the ellipsoid into a mesh of squares (of varying size). The isometric latitude is zero at the equator but rapidly diverges from the geodetic latitude, tending to infinity at the poles. The conventional notation is given in Snyder (page 15):

${\begin{aligned}\psi (\phi )&=\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\phi }{2}}\right)\right]+{\frac {e}{2}}\ln \left[{\frac {1-e\sin \phi }{1+e\sin \phi }}\right]\\&=\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\\&=\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi ).\end{aligned}}$

For the normal Mercator projection (on the ellipsoid) this function defines the spacing of the parallels: if the length of the equator on the projection is E (units of length or pixels) then the distance, y, of a parallel of latitude ϕ from the equator is

$y(\phi )={\frac {E}{2\pi }}\psi (\phi )\,.$

The isometric latitude ψ is closely related to the conformal latitude χ:

$\psi (\phi )=\operatorname {gd} ^{-1}\chi (\phi )\,.$

Inverse formulae and series

The formulae in the previous sections give the auxiliary latitude in terms of the geodetic latitude. The expressions for the geocentric and parametric latitudes may be inverted directly but this is impossible in the four remaining cases: the rectifying, authalic, conformal, and isometric latitudes. There are two methods of proceeding.

• The first is a numerical inversion of the defining equation for each and every particular value of the auxiliary latitude. The methods available are fixed-point iteration and Newton–Raphson root finding.
  • When converting from isometric or conformal to geodetic, two iterations of Newton-Raphson gives double precision accuracy.
• The other, more useful, approach is to express the auxiliary latitude as a series in terms of the geodetic latitude and then invert the series by the method of Lagrange reversion. Such series are presented by Adams who uses Taylor series expansions and gives coefficients in terms of the eccentricity. Orihuela gives series for the conversions between all pairs of auxiliary latitudes in terms of the third flattening, n = (a - b)/(a + b). Karney establishes that the truncation errors for such series are consistently smaller that the equivalent series in terms of the eccentricity. The series method is not applicable to the isometric latitude and one must find the conformal latitude in an intermediate step.

Numerical comparison of auxiliary latitudes

inline

The plot to the right shows the difference between the geodetic latitude and the auxiliary latitudes other than the isometric latitude (which diverges to infinity at the poles) for the case of the WGS84 ellipsoid. The differences shown on the plot are in arc minutes. In the Northern hemisphere (positive latitudes), θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ϕ; in the Southern hemisphere (negative latitudes), the inequalities are reversed, with equality at the equator and the poles. Although the graph appears symmetric about 45°, the minima of the curves actually lie between 45° 2′ and 45° 6′. Some representative data points are given in the table below. The conformal and geocentric latitudes are nearly indistinguishable, a fact that was exploited in the days of hand calculators to expedite the construction of map projections.

To first order in the flattening f, the auxiliary latitudes can be expressed as

ζ = ϕ − Cf sin 2ϕ where the constant C takes on the values [1⁄2, 2⁄3, 3⁄4, 1, 1] for ζ = [β, ξ, μ, χ, θ].

Approximate difference from geodetic latitude (ϕ)

ϕ	Parametric β − ϕ	Authalic ξ − ϕ	Rectifying μ − ϕ	Conformal χ − ϕ	Geocentric θ − ϕ
0°	0.00′	0.00′	0.00′	0.00′	0.00′
15°	−2.88′	−3.84′	−4.32′	−5.76′	−5.76′
30°	−5.00′	−6.66′	−7.49′	−9.98′	−9.98′
45°	−5.77′	−7.70′	−8.66′	−11.54′	−11.55′
60°	−5.00′	−6.67′	−7.51′	−10.01′	−10.02′
75°	−2.89′	−3.86′	−4.34′	−5.78′	−5.79′
90°	0.00′	0.00′	0.00′	0.00′	0.00′

Latitude and coordinate systems

The geodetic latitude, or any of the auxiliary latitudes defined on the reference ellipsoid, constitutes with longitude a two-dimensional coordinate system on that ellipsoid. To define the position of an arbitrary point it is necessary to extend such a coordinate system into three dimensions. Three latitudes are used in this way: the geodetic, geocentric and parametric latitudes are used in geodetic coordinates, spherical polar coordinates and ellipsoidal coordinates respectively.

Geodetic coordinates

Main article: Geodetic coordinates

Geodetic coordinates P(ɸ,λ,h)

At an arbitrary point P consider the line PN which is normal to the reference ellipsoid. The geodetic coordinates P(ɸ,λ,h) are the latitude and longitude of the point N on the ellipsoid and the distance PN. This height differs from the height above the geoid or a reference height such as that above mean sea level at a specified location. The direction of PN will also differ from the direction of a vertical plumb line. The relation of these different heights requires knowledge of the shape of the geoid and also the gravity field of the Earth.

Spherical polar coordinates

Geocentric coordinate related to spherical polar coordinates P(r,θ′,λ)

The geocentric latitude θ is the complement of the polar angle or colatitude θ′ in conventional spherical polar coordinates in which the coordinates of a point are P(r,θ′,λ) where r is the distance of P from the centre O, θ′ is the angle between the radius vector and the polar axis and λ is longitude. Since the normal at a general point on the ellipsoid does not pass through the centre it is clear that points P' on the normal, which all have the same geodetic latitude, will have differing geocentric latitudes. Spherical polar coordinate systems are used in the analysis of the gravity field.

Ellipsoidal-harmonic coordinates

Ellipsoidal coordinates P(u,β,λ)

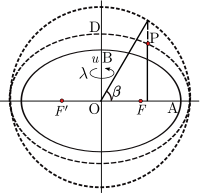
The parametric latitude can also be extended to a three-dimensional coordinate system. For a point P not on the reference ellipsoid (semi-axes OA and OB) construct an auxiliary ellipsoid which is confocal (same foci F, F′) with the reference ellipsoid: the necessary condition is that the product ae of semi-major axis and eccentricity is the same for both ellipsoids. Let u be the semi-minor axis (OD) of the auxiliary ellipsoid. Further let β be the parametric latitude of P on the auxiliary ellipsoid. The set (u,β,λ) define the ellipsoidal-harmonic coordinates or simply ellipsoidal coordinates (although that term is also used to refer to geodetic coordinate). These coordinates are the natural choice in models of the gravity field for a rotating ellipsoidal body. The above applies to a biaxial ellipsoid (a spheroid, as in oblate spheroidal coordinates); for a generalization, see triaxial ellipsoidal coordinates.

Coordinate conversions

The relations between the above coordinate systems, and also Cartesian coordinates are not presented here. The transformation between geodetic and Cartesian coordinates may be found in geographic coordinate conversion. The relation of Cartesian and spherical polars is given in spherical coordinate system. The relation of Cartesian and ellipsoidal coordinates is discussed in Torge.

Astronomical latitude

1. Ocean
2. Ellipsoid
3. Local plumb line
4. Continent
5. Geoid

Astronomical latitude (Φ) is the angle between the equatorial plane and the true vertical direction at a point on the surface. The true vertical, the direction of a plumb line, is also the gravity direction (the resultant of the gravitational acceleration (mass-based) and the centrifugal acceleration) at that latitude. Astronomic latitude is calculated from angles measured between the zenith and stars whose declination is accurately known.

In general the true vertical at a point on the surface does not exactly coincide with either the normal to the reference ellipsoid or the normal to the geoid. The geoid is an idealized, theoretical shape "at mean sea level". Points on land do not lie precisely on the geoid, and the vertical at a point at a specific time is influenced by tidal forces which the theoretical geoid averages out. The angle between the astronomic and geodetic normals is called vertical deflection and is usually a few seconds of arc but it is important in geodesy.

Astronomical latitude is not to be confused with declination, the coordinate astronomers use in a similar way to specify the angular position of stars north–south of the celestial equator (see equatorial coordinates), nor with ecliptic latitude, the coordinate that astronomers use to specify the angular position of stars north–south of the ecliptic (see ecliptic coordinates).

See also

• Altitude (mean sea level)
• Bowditch's American Practical Navigator
• Cardinal direction
• Circle of latitude
• Colatitude
• Declination on celestial sphere
• Degree Confluence Project
• Geodesy
• Geodetic datum
• Geographic coordinate system
• Geographical distance
• Geomagnetic latitude
• Geotagging
• Great-circle distance
• History of latitude
• Horse latitudes
• International Latitude Service
• List of countries by latitude
• Longitude
• Natural Area Code
• Navigation
• Orders of magnitude (length)
• World Geodetic System

External links

• GEONets Names Server. Archived 2008-03-09 at the Wayback Machine. access to the National Geospatial-Intelligence Agency's (NGA) database of foreign geographic feature names.
• Resources for determining your latitude and longitude Archived 2008-05-19 at the Wayback Machine
• Convert decimal degrees into degrees, minutes, seconds. Archived 2012-11-07 at the Wayback Machine – info about decimal to sexagesimal conversion.
• Convert decimal degrees into degrees, minutes, seconds
• Distance calculation based on latitude and longitude – JavaScript version
• 16th Century Latitude Survey
• Determination of Latitude by Francis Drake on the Coast of California in 1579

For other uses, see Longitude (disambiguation).

A graticule on the Earth as a sphere or an ellipsoid. The lines from pole to pole are lines of constant longitude, or meridians. The circles parallel to the Equator are circles of constant latitude, or parallels. The graticule shows the latitude and longitude of points on the surface. In this example, meridians are spaced at 6° intervals and parallels at 4° intervals.

Longitude (/ˈlɒndʒɪtjuːd/, AU and UK also /ˈlɒŋɡɪ-/) is a geographic coordinate that specifies the east–west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are imaginary semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, south-east London on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west.

Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absolute measure of time allows longitude to be determined. Depending on the era, the absolute time might be obtained from a celestial event visible from both locations, such as a lunar eclipse, or from a time signal transmitted by telegraph or radio. The principle is straightforward, but in practice finding a reliable method of determining longitude took centuries and required the effort of some of the greatest scientific minds.

A location's north–south position along a meridian is given by its latitude, which is approximately the angle between the equatorial plane and the normal from the ground at that location.

Longitude is generally given using the geodetic normal or the gravity direction. The astronomical longitude can differ slightly from the ordinary longitude because of vertical deflection, small variations in Earth's gravitational field (see astronomical latitude).

History

Main article: History of longitude

The concept of longitude was first developed by ancient Greek astronomers. Hipparchus (2nd century BCE) used a coordinate system that assumed a spherical Earth, and divided it into 360° as we still do today. His prime meridian passed through Alexandria. He also proposed a method of determining longitude by comparing the local time of a lunar eclipse at two different places, thus demonstrating an understanding of the relationship between longitude and time. Claudius Ptolemy (2nd century CE) developed a mapping system using curved parallels that reduced distortion. He also collected data for many locations, from Britain to the Middle East. He used a prime meridian through the Canary Islands, so that all longitude values would be positive. While Ptolemy's system was sound, the data he used were often poor, leading to a gross over-estimate (by about 70%) of the length of the Mediterranean.

After the fall of the Roman Empire, interest in geography greatly declined in Europe. Hindu and Muslim astronomers continued to develop these ideas, adding many new locations and often improving on Ptolemy's data. For example al-Battānī used simultaneous observations of two lunar eclipses to determine the difference in longitude between Antakya and Raqqa with an error of less than 1°. This is considered to be the best that can be achieved with the methods then available: observation of the eclipse with the naked eye, and determination of local time using an astrolabe to measure the altitude of a suitable "clock star".

In the later Middle Ages, interest in geography revived in the west, as travel increased, and Arab scholarship began to be known through contact with Spain and North Africa. In the 12th century, astronomical tables were prepared for a number of European cities, based on the work of al-Zarqālī in Toledo. The lunar eclipse of September 12, 1178 was used to establish the longitude differences between Toledo, Marseilles, and Hereford.

Christopher Columbus made two attempts to use lunar eclipses to discover his longitude, the first in Saona Island, on 14 September 1494 (second voyage), and the second in Jamaica on 29 February 1504 (fourth voyage). It is assumed that he used astronomical tables for reference. His determinations of longitude showed large errors of 13° and 38° W respectively. Randles (1985) documents longitude measurement by the Portuguese and Spanish between 1514 and 1627 both in the Americas and Asia. Errors ranged from 2° to 25°.

The telescope was invented in the early 17th century. Initially an observation device, developments over the next half century transformed it into an accurate measurement tool. The pendulum clock was patented by Christiaan Huygens in 1657 and gave an increase in accuracy of about 30 fold over previous mechanical clocks. These two inventions would revolutionise observational astronomy and cartography.

On land, the period from the development of telescopes and pendulum clocks until the mid-18th century saw a steady increase in the number of places whose longitude had been determined with reasonable accuracy, often with errors of less than a degree, and nearly always within 2° to 3°. By the 1720s errors were consistently less than 1°. At sea during the same period, the situation was very different. Two problems proved intractable. The first was the need of a navigator for immediate results. The second was the marine environment. Making accurate observations in an ocean swell is much harder than on land, and pendulum clocks do not work well in these conditions.

The chronometer

The clockwork in John Harrison's H4 marine chronometer on display at the Royal Observatory, Greenwich

In response to the problems of navigation, a number of European maritime powers offered prizes for a method to determine longitude at sea. The best-known of these is the Longitude Act passed by the British parliament in 1714. It offered two levels of rewards, for solutions within 1° and 0.5°. Rewards were given for two solutions: lunar distances, made practicable by the tables of Tobias Mayer developed into an nautical almanac by the Astronomer Royal Nevil Maskelyne; and for the chronometers developed by the Yorkshire carpenter and clock-maker John Harrison. Harrison built five chronometers over more than three decades. This work was supported and rewarded with thousands of pounds from the Board of Longitude, but he fought to receive money up to the top reward of £20,000, finally receiving an additional payment in 1773 after the intervention of parliament. It was some while before either method became widely used in navigation. In the early years, chronometers were very expensive, and the calculations required for lunar distances were still complex and time-consuming. Lunar distances came into general use after 1790. Chronometers had the advantages that both the observations and the calculations were simpler, and as they became cheaper in the early 19th century they started to replace lunars, which were seldom used after 1850.

The first working telegraphs were established in Britain by Wheatstone and Cooke in 1839, and in the US by Morse in 1844. It was quickly realised that the telegraph could be used to transmit a time signal for longitude determination. The method was soon in practical use for longitude determination, especially in North America, and over longer and longer distances as the telegraph network expanded, including western Europe with the completion of transatlantic cables. The United States Coast Survey, renamed the United States Coast and Geodetic Survey in 1878, was particularly active in this development, and not just in the United States. The Survey established chains of mapped locations through Central and South America, and the West Indies, and as far as Japan and China in the years 1874–90. This contributed greatly to the accurate mapping of these areas.

While mariners benefited from the accurate charts, they could not receive telegraph signals while under way, and so could not use the method for navigation. This changed when wireless telegraphy (radio) became available in the early 20th century. Wireless time signals for the use of ships were transmitted from Halifax, Nova Scotia, starting in 1907 and from the Eiffel Tower in Paris from 1910. These signals allowed navigators to check and adjust their chronometers frequently.

Radio navigation systems came into general use after World War II. The systems all depended on transmissions from fixed navigational beacons. A ship-board receiver calculated the vessel's position from these transmissions. They allowed accurate navigation when poor visibility prevented astronomical observations, and became the established method for commercial shipping until replaced by GPS in the early 1990s.

Determination

Further information: Celestial navigation § Longitude

See also: Latitude determination

The main conventional methods for determining longitude are listed below. With one exception (magnetic declination), they all depend on a common principle, which is to determine the time for an event or measurement and to compare it with the time at a different location. Longitude, being up to 180° east or west of a prime meridian, is mathematically related to time differences up to 12 hours by a factor of 15. Thus, a time differential (in hours) between two points is multiplied by 15 to obtain a longitudinal difference (in degrees).

Historically, times used for calculating longitude have included apparent solar time, local mean time, and ephemeris time, with mean time being the one most used for navigation of the sea. See also the equation of time for details on the differences.

• Lunar distances and moon culminations. In its orbit around the Earth, the Moon moves relative to the stars at a rate of just over 0.5°/hour. The angle between the limb of the Moon and a suitable star, planet, or sun is measured with a sextant, and, after consulting ephemeris tables, a value for the mean time at a reference meridian, usually Greenwich, can be calculated. For a culmination, the observer simply records the time and compares it with the reference time in the ephemerides after correcting for refraction and other errors. This method was established by Nathaniel Pigott around 1786. The Nautical Almanac was published in the UK beginning in 1767 and the American Ephemeris and Nautical Almanac starting in 1852.
• Satellites of Jupiter. Galileo proposed that with sufficiently accurate knowledge of the orbits of the satellites, their positions could provide a measure of absolute time. The method requires a telescope, as the moons are not visible to the naked eye. Ephemeris tables are employed for comparison to a reference meridian.
• Appulses, occultations, transits, and eclipses. An appulse is the least apparent distance between two objects (the Moon, a star or a planet); an occultation occurs when a star or planet passes behind the Moon — essentially a type of eclipse. Lunar eclipses continued to be used. The times of these events are compared to those of a reference meridian. Major observatories used the transit circle or meridian circle to establish very accurate longitude values for their country, often establishing their own prime meridian at the longitude of the instrument.
• Transport of chronometers. A clock is set to the local time of a starting point whose longitude is known, and the longitude of any other place can be determined by comparing its local mean time with the clock time. While marine chronometers are relatively stable, they are also relatively large and expensive. Prior to the quartz crystal, chronometers were susceptible to time drift from temperature fluctuations and vibration.
• Signals. Rockets and lights were occasionally used in the 18th and 19th century, although the method is impractical except for short distances and demonstrations. It was a rudimentary form of synchronizing time and establishing longitude. However, signaling by "ball drop" was extensively used in the US Navy and Royal Navy in the 19th century. In each case, there were observatories near bodies of water that would drop a ball from a tower, alerting the ships of the correct time, and hence enabling them to maintain stable longitudinal position fixes while at sea.
• Telegraphic determination of longitude. First suggested by the American astronomer Sears Cook Walker, the United States Coast Survey began deploying it in 1849. Europe quickly followed. As the American West was settled, mapping and surveying was greatly improved by the use of the telegraph to determine time and longitude differences between stations. The laying of transatlantic telegraph cables also helped establish coordinated global mapping and navigation.
• Magnetic declination. A compass needle does not in general point true north. The variation from true north varies with location, and it was suggested that this could provide a basis for determination of longitude.

With the exception of magnetic declination, all proved practicable methods. Developments on land and sea, however, were very different.

Several newer methods for navigation, location finding, and the determination of longitude exist. Radio navigation, satellite navigation, and Inertial navigation systems, along with celestial navigation, are a few of the more prevalent ones.

Values

Longitude is given as an angular measurement with 0° at the Prime Meridian, ranging from −180° westward to +180° eastward. The Greek letter λ (lambda) is used to denote the location of a place on Earth east or west of the Prime Meridian.

Each degree of longitude is sub-divided into 60 minutes, each of which is divided into 60 seconds. A longitude is thus specified in sexagesimal notation as, for example, 23° 27′ 30″ E. For higher precision, the seconds are specified with a decimal fraction. An alternative representation uses degrees and minutes, and parts of a minute are expressed in decimal notation, thus: 23° 27.5′ E. Degrees may also be expressed as a decimal fraction: 23.45833° E. For calculations, the angular measure may be converted to radians, so longitude may also be expressed in this manner as a signed fraction of π (pi), or an unsigned fraction of 2π.

For calculations, the west/east suffix is replaced by a negative sign in the western hemisphere. The international standard convention (ISO 6709)—that east is positive—is consistent with a right-handed Cartesian coordinate system, with the North Pole up. A specific longitude may then be combined with a specific latitude (positive in the northern hemisphere) to give a precise position on the Earth's surface. Confusingly, the convention of negative for east is also sometimes seen, most commonly in the United States; the Earth System Research Laboratories used it on an older version of one of their pages, in order "to make coordinate entry less awkward" for applications confined to the Western Hemisphere. They have since shifted to the standard approach.

The longitude is singular at the Poles and calculations that are sufficiently accurate for other positions may be inaccurate at or near the Poles. Also the discontinuity at the ±180° meridian must be handled with care in calculations. An example is a calculation of east displacement by subtracting two longitudes, which gives the wrong answer if the two positions are on either side of this meridian. To avoid these complexities, some applications use another horizontal position representation.

Length of a degree of longitude

See also: Length of a degree of latitude

The length of a degree of longitude (east–west distance) depends only on the radius of a circle of latitude. For a sphere of radius a that radius at latitude φ is a cos φ, and the length of a one-degree (or ⁠π/180⁠ radian) arc along a circle of latitude is

$\Delta _{\rm {long}}^{1}={\frac {\pi }{180}}a\cos \phi$

φ	Δ1 lat	Δ1 long
0°	110.574 km	111.320 km
15°	110.649 km	107.551 km
30°	110.852 km	96.486 km
45°	111.133 km	78.847 km
60°	111.412 km	55.800 km
75°	111.618 km	28.902 km
90°	111.694 km	0.000 km

Length of one degree (black), minute (blue) and second (red) of latitude and longitude in metric (upper half) and imperial units (lower half) at a given latitude (vertical axis) in WGS84. For example, the green arrows show that Donetsk (green circle) at 48°N has a Δ_long of 74.63 km/° (1.244 km/min, 20.73 m/sec etc) and a Δ_lat of 111.2 km/° (1.853 km/min, 30.89 m/sec etc).

When the Earth is modelled by an ellipsoid this arc length becomes

$\Delta _{\rm {long}}^{1}={\frac {\pi a\cos \phi }{180{\sqrt {1-e^{2}\sin ^{2}\phi }}}}$

where e, the eccentricity of the ellipsoid, is related to the major and minor axes (the equatorial and polar radii respectively) by

$e^{2}={\frac {a^{2}-b^{2}}{a^{2}}}$

An alternative formula is

$\Delta _{\rm {long}}^{1}={\frac {\pi }{180}}a\cos \beta \quad {\mbox{where }}\tan \beta ={\frac {b}{a}}\tan \phi$; here $\beta$ is the so-called parametric or reduced latitude.

cos φ decreases from 1 at the equator to 0 at the poles, which measures how circles of latitude shrink from the equator to a point at the pole, so the length of a degree of longitude decreases likewise. This contrasts with the small (1%) increase in the length of a degree of latitude (north–south distance), equator to pole. The table shows both for the WGS84 ellipsoid with a = 6378137.0 m and b = 6356752.3142 m. The distance between two points 1 degree apart on the same circle of latitude, measured along that circle of latitude, is slightly more than the shortest (geodesic) distance between those points (unless on the equator, where these are equal); the difference is less than 0.6 m (2 ft).

A geographical mile is defined to be the length of one minute of arc along the equator (one equatorial minute of longitude) therefore a degree of longitude along the equator is exactly 60 geographical miles or 111.3 kilometers, as there are 60 minutes in a degree. The length of 1 minute of longitude along the equator is 1 geographical mile or 1.855 km or 1.153 miles, while the length of 1 second of it is 0.016 geographical mile or 30.916 m or 101.43 feet.

See also

• American Practical Navigator
• Cardinal direction
• Dead reckoning
• Ecliptic longitude
• Geodesy
• Geodetic system
• Geographic coordinate system
• Geographical distance
• Geotagging
• Great-circle distance
• History of longitude
• The Island of the Day Before
• Latitude
• Meridian arc
• Natural Area Code
• Navigation
• Orders of magnitude
• Planetary coordinate system#Longitude
• Right ascension on celestial sphere
• World Geodetic System

Further reading

• Andrews, William J. H. (1996). The Quest for Longitude. Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-9644329-0-1. OCLC 59617314.
• Howse, Derek (1980). Greenwich Time and the Discovery of the Longitude. Philip Wilson Publishers, Ltd. ISBN 978-0-19-215948-9.

External links

• Resources for determining your latitude and longitude Archived 2008-05-19 at the Wayback Machine
• IAU/IAG Working Group On Cartographic Coordinates and Rotational Elements of the Planets and Satellites Archived 2006-04-06 at the Wayback Machine
• "Longitude forged": an essay exposing a hoax solution to the problem of calculating longitude, undetected in Dava Sobel's Longitude, from TLS, November 12, 2008.
• Board of Longitude Collection, Cambridge Digital Library – complete digital version of the Board's archive
• Longitude And Latitude Of Points of Interest
• Length Of A Degree Of Latitude And Longitude Calculator
• Esame critico intorno alla scoperta di Vespucci ...
• A land beyond the stars - Museo Galileo